CS32: Advances in Statistical Inference for Spatial Point Processes
date: 7/17/2025, time: 14:00-15:30, room: ICS 119
Organizer: Bartlomiej Blaszczyszyn (Inria/ENS)
Chair: Bartlomiej Blaszczyszyn (Inria/ENS)
Minimax Estimation of the Structure Factor of Spatial Point Processes
Gabriel Mastrilli (Ensai Rennes, Inria Paris)
Spectral methods have recently gained attention in spatial statistics as an alternative to direct-space techniques for second-order inference of spatial point processes. Instead of analyzing second-order summary statistics like the Ripley K-function, one can estimate Bartlett’s spectral measure, also known in physics as the structure factor \(S\), which is the Fourier transform of the pair correlation function. Several estimators of \(S\) have been introduced \([1, 2, 3]\). However, without a reference minimax rate of convergence, it remains unclear whether better estimators could be constructed.
We address this gap by proving the following minimax result: for estimating a structure factor of Hölder regularity \(\beta\), the worst-case error of any estimator is at least the expected number of observed points raised to the power \(-\beta/(2\beta + d)\). We then construct multi-taper estimators that achieve this optimal rate and further show that they exhibit exponential concentration. These estimators are oracle in the sense that they depend on unknown parameters related to the smoothness of \(S\). To obtain a practical estimator, we propose a cross-validation method based on random thinning and decorrelation between distinct frequencies.
Bibliography
\([1]\) D. Hawat, G. Gautier, R. Bardenet and R. Lachièze-Rey, "On estimating the structure factor of a point process, with applications to hyperuniformity", Statistics and Computing, 2023.
\([2]\) T. Rajala, S. Olhede, J. P Grainger, and D. J Murrell, "What is the Fourier transform of a spatial point process ?", IEEE Transactions on Information Theory, 2023.
\([3]\) J. Yang and Y. Guan,"Fourier analysis of spatial point processes", arXiv:2401.06403, 2024.
Estimating the hyperuniformity exponent of point processes
Bartlomiej Blaszczyszyn (Inria/ENS)
Hyperuniformity characterizes random spatial structures whose large-scale variance grows more slowly than that of Poisson processes. First introduced in statistical physics by Torquato and Stillinger \([1]\), hyperuniform systems have attracted considerable attention due to their intermediate nature between perfect crystals, liquids, and glasses, and appears in a wide range of applications, from DNA organization and immune system dynamics to photoreceptor arrangements, urban planning, and cosmology.
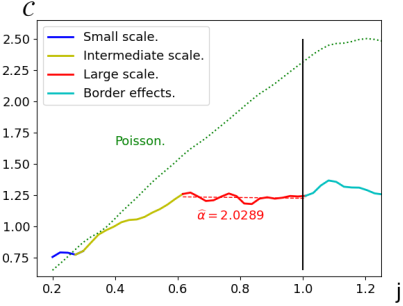
Detecting and quantifying hyperuniformity is essential across these diverse fields. Yet, statistical testing for hyperuniformity has only recently begun to develop. In joint work \([2]\), we address the problem of estimating the “strength” of hyperuniformity—formally, the exponent governing the decay of the spectral density near zero frequency—in a class of stationary point processes in Euclidean space. The key mathematical idea is that the variance of linear statistics, defined using smooth, rapidly decaying test functions, grows in a way that explicitly reflects this exponent. Using a multivariate central limit theorem for a family of such statistics, constructed from orthogonal functions at multiple scales (e.g., wavelets), we derive an asymptotically consistent estimator of the strength of hyperuniformity. This estimator can be computed from a single realization of the point process and comes with explicit confidence intervals. We validate this approach through simulations of various point process models and demonstrate its applicability on real data.
image

image
We estimated the hyperuniformity exponent \(\alpha\) for the Ginibre point process in two dimensions, using 75 Hermitian wavelets (\(f_i\)). This process is known to have an exponent of \(\alpha=2\). The estimation result is shown on the left, and the point process itself (with 1600 points) on the right. The estimator of the hyperuniformity exponent \(\widehat{\alpha} = \text{dimension }d - \text{slope of } \mathcal{C}\), where \(\mathcal{C}: j \mapsto \frac{1}{\log(R)} \log \left( \sum_{i \in I} \left( \sum_{x \in \Phi \cap [-R, R]^d} f_i\left(x/R^j\right) \right)^2 \right)\).
Bibliography
\([1]\) Torquato, S. and Stillinger, F. H. (2003). Local density fluctuations, hyperuniformity, and order metrics. Physical Review E 68 041113.
\([2]\) Mastrilli, G., Błaszczyszyn, B. and Lavancier, F. (2024) Estimating the hyperuniformity exponent of point processes arXiv:2407.16797.
Conformal Novelty Detection for Replicate Point Patterns
Christophe Biscio (University of Aalborg)
Monte Carlo tests are widely used for computing valid p-values without requiring known distributions of test statistics. When performing multiple Monte Carlo tests, it is essential to maintain control of the type I error. Some techniques for multiplicity control pose requirements on the joint distribution of the p-values, for instance independence, which can be computationally intensive to achieve using naïve multiple Monte Carlo testing.
We highlight in this work that multiple Monte Carlo testing is an instance of conformal novelty detection. Leveraging this insight enables a more efficient multiple Monte Carlo testing procedure, avoiding excessive simulations while still ensuring exact control over the false discovery rate or the family-wise error rate. We call this approach conformal multiple Monte Carlo testing.
The performance is investigated in the context of global envelope tests for point pattern data through a simulation study and an application to a sweat gland data set. Results reveal that with a fixed number of simulations under the null hypothesis, our proposed method yields substantial improvements in power of the testing procedure as compared to the naïve multiple Monte Carlo testing procedure.
Bibliography
\([1]\) Christophe A.N. Biscio and Adrien Mazoyer and Martin V. Vejling. "Conformal novelty detection for replicate point patterns with FDR or FWER control." arXiv: 2501.18195.